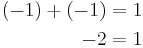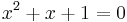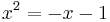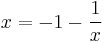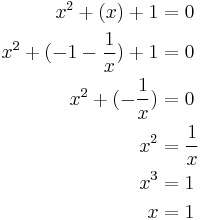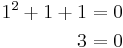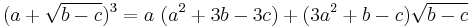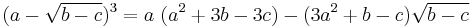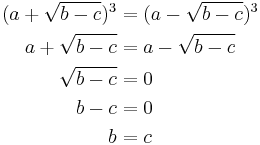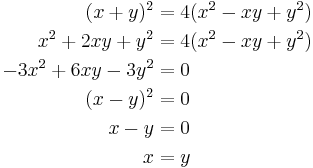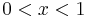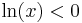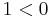Mathematical fallacy
In mathematics, certain kinds of mistakes in proof, calculation, or derivation are often exhibited, and sometimes collected, as illustrations of the concept of mathematical fallacy. The specimens of the greatest interest can be seen as entertaining, or of substantial educational value.
Contents |
The Mistake, the Howler and the Fallacy
Perhaps the first really prominent modern treatment of the subject was Fallacies in mathematics (1963) by E. A. Maxwell.[1] He drew a distinction between a simple mistake, a howler and a mathematical fallacy. He dismissed mere mistakes as being "of little interest and, one hopes, of even less consequence". In the modern world we have seen examples where errors have been of grave consequence, but still not of interest in the present context.
Mistakes in general could of course be of great interest in other fields, such as the study of error proneness, security, and error detection and correction.
Maxwell had more to say on what he called "fallacies" and "howlers": "The howler in mathematics is not easy to describe, but the term may be used to denote an error which leads innocently to a correct result. By contrast, the fallacy leads by guile to a wrong but plausible conclusion.
In the best-known examples of mathematical fallacies, there is some concealment in the presentation of the proof. For example the reason validity fails may be a division by zero that is hidden by algebraic notation. There is a striking quality of the mathematical fallacy: as typically presented, it leads not only to an absurd result, but does so in a crafty or clever way.[2] Therefore these fallacies, for pedagogic reasons, usually take the form of spurious proofs of obvious contradictions. Although the proofs are flawed, the errors, usually by design, are comparatively subtle, or designed to show that certain steps are conditional, and should not be applied in the cases that are the exceptions to the rules.
The traditional way of presenting a mathematical fallacy is to give an invalid step of deduction mixed in with valid steps, so that the meaning of fallacy is here slightly different from the logical fallacy. The latter applies normally to a form of argument that is not a genuine rule of logic, where the problematic mathematical step is typically a correct rule applied with a tacit wrong assumption. Beyond pedagogy, the resolution of a fallacy can lead to deeper insights into a subject (such as the introduction of Pasch's axiom of Euclidean geometry).[3] Pseudaria, an ancient lost book of false proofs, is attributed to Euclid.[4]
Mathematical fallacies exist in many branches of mathematics. In elementary algebra, typical examples may involve a step where division by zero is performed, where a root is incorrectly extracted or, more generally, where different values of a multiple valued function are equated. Well-known fallacies also exist in elementary Euclidean geometry and calculus.
Howlers
A correct result obtained by an incorrect line of reasoning is an example of a mathematical argument that is true but invalid. This is the case, for instance, in the calculation
Although the conclusion 16/64 = 1/4 is correct, there is a fallacious invalid cancellation in the middle step. Bogus proofs constructed to produce a correct result in spite of incorrect logic are described as howlers by Maxwell.[5]
Division by zero
The division-by-zero fallacy has many variants.
All numbers equal all other numbers
The following example uses division by zero to "prove" that 2 = 1, but can be modified to prove that any number equals any other number.
1. Let a and b be equal non-zero quantities
2. Multiply through by a
3. Subtract 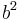
4. Factor both sides
5. Divide out 
6. Observing that 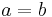
7. Combine like terms on the left
8. Divide by the non-zero b
The fallacy is in line 5: the progression from line 4 to line 5 involves division by a − b, which is zero since a equals b. Since division by zero is undefined, the argument is invalid. Deriving that the only possible solution for lines 5, 6, and 7, namely that a = b = 0, this flaw is evident again in line 7, where one must divide by b (0) in order to produce the fallacy (not to mention that the only possible solution denies the original premise that a and b are nonzero). A similar invalid proof would be to say that since 2 × 0 = 1 × 0 (which is true), one can divide by zero to obtain 2 = 1. An obvious modification "proves" that any two real numbers are equal.
Many variants of this fallacy exist. For instance, it is possible to attempt to "repair" the proof by supposing that a and b have a definite nonzero value to begin with, for instance, at the outset one can suppose that a and b are both equal to one:
However, as already noted the step in line 5, when the equation is divided by a − b, is still division by zero. As division by zero is undefined, the argument is invalid.
Multivalued functions
Functions that are multivalued have poorly defined inverse functions over their entire range.
Multivalued sinusoidal functions
We are going to prove that 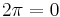 :
:
The problem is in the third step, where we take the arcsin of each side. Since the arcsin is an infinitely multivalued function, 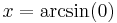 need not be true even if
need not be true even if 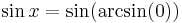 .
.
Multivalued complex logarithms
We are going to prove that 1 = 3. From Euler's formula we see that
and
so we have
Taking logarithms gives
and hence
Dividing by πi gives
Q.E.D.
The mistake is that the rule 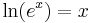 is in general only valid for real x, not for complex x. The complex logarithm is actually multi-valued; and
is in general only valid for real x, not for complex x. The complex logarithm is actually multi-valued; and 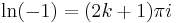 for any integer k, so we see that
for any integer k, so we see that 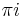 and
and 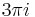 are two among the infinite possible values for ln(-1).
are two among the infinite possible values for ln(-1).
Calculus
Calculus as the mathematical study of infinitesimal change and limits can lead to mathematical fallacies if the properties of integrals and differentials are ignored.
Indefinite integrals
The following "proof" that 0 = 1 can be modified to "prove" that any number equals any other number. Begin with the evaluation of the indefinite integral
Through integration by parts, let
Thus,
Hence, by integration by parts
The error in this proof lies in an improper use of the integration by parts technique. Upon use of the formula, a constant, C, must be added to the right-hand side of the equation. This is due to the derivation of the integration by parts formula; the derivation involves the integration of an equation and so a constant must be added. In most uses of the integration by parts technique, this initial addition of C is ignored until the end when C is added a second time. However, in this case, the constant must be added immediately because the remaining two integrals cancel each other out.
In other words, the second to last line is correct (1 added to any antiderivative of 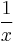 is still an antiderivative of
is still an antiderivative of 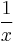 ); but the last line is not. You cannot cancel
); but the last line is not. You cannot cancel 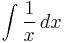 because they are not necessarily equal. There are infinitely many antiderivatives of a function, all differing by a constant. In this case, the antiderivatives on both sides differ by 1.
because they are not necessarily equal. There are infinitely many antiderivatives of a function, all differing by a constant. In this case, the antiderivatives on both sides differ by 1.
This problem can be avoided if we use definite integrals (i.e. use bounds). Then in the second to last line, 1 would be evaluated between some bounds, which would always evaluate to 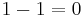 . The remaining definite integrals on both sides would indeed be equal.
. The remaining definite integrals on both sides would indeed be equal.
Variable ambiguity
We are going to prove that 1 = 0. Take the statement
Taking the derivative of each side,
The derivative of x is 1, and the derivative of 1 is 0. Therefore,
Q.E.D.
The error in this proof is it treats x as a variable, and not as a constant as stated by x = 1 in the proof, when taking the derivative with respect to x. Since there is no such thing as differentiating with respect to a constant, differentiating both sides with respect to x (which is a constant) is an invalid step.
Infinite series
As in the case of surreal and aleph numbers, mathematical situations which involve manipulation of infinite series can lead to logical contradictions if care is not taken to remember the properties of such series.
Associative law
We are going to prove that 1 = 0. Start with the addition of an infinite succession of zeros
Then recognize that 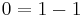
Applying the associative law of addition results in
Of course 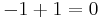
And the addition of an infinite string of zeros can be discarded leaving
Q.E.D.
The error here is that the associative law cannot be applied freely to an infinite sum unless the sum is absolutely convergent (see also conditionally convergent). Here that sum is 1 − 1 + 1 − 1 + · · ·, a classic divergent series. In this particular argument, the second line gives the sequence of partial sums 0, 0, 0, ... (which converges to 0) while the third line gives the sequence of partial sums 1, 1, 1, ... (which converges to 1), so these expressions need not be equal. This can be seen as a counterexample to generalizing Fubini's theorem and Tonelli's theorem to infinite integrals (sums) over measurable functions taking negative values.
In fact the associative law for addition just states something about three-term sums:  . It can easily be shown to imply that for any finite sequence of terms separated by "+" signs, and any two ways to insert parentheses so as to completely determine which are the operands of each "+", the sums have the same value; the proof is by induction on the number of additions involved. In the given "proof" it is in fact not so easy to see how to start applying the basic associative law, but with some effort one can arrange larger and larger initial parts of the first summation to look like the second. However this would take an infinite number of steps to "reach" the second summation completely. So the real error is that the proof compresses infinitely many steps into one, while a mathematical proof must consist of only finitely many steps. To illustrate this, consider the following "proof" of
. It can easily be shown to imply that for any finite sequence of terms separated by "+" signs, and any two ways to insert parentheses so as to completely determine which are the operands of each "+", the sums have the same value; the proof is by induction on the number of additions involved. In the given "proof" it is in fact not so easy to see how to start applying the basic associative law, but with some effort one can arrange larger and larger initial parts of the first summation to look like the second. However this would take an infinite number of steps to "reach" the second summation completely. So the real error is that the proof compresses infinitely many steps into one, while a mathematical proof must consist of only finitely many steps. To illustrate this, consider the following "proof" of 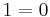 that only uses convergent infinite sums, and only the law allowing to interchange two consecutive terms in such a sum, which is definitely valid:
that only uses convergent infinite sums, and only the law allowing to interchange two consecutive terms in such a sum, which is definitely valid:
Divergent series
Define the constants S and A by
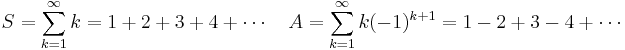 .
.
Therefore
Adding these two equations gives
Therefore, the sum of all positive integers is negative.
A variant of mathematical fallacies of this form involves the p-adic numbers
Let 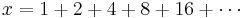 .
.
Then, 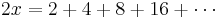 .
.
Subtracting these two equations produces 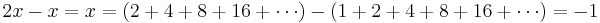 .
.
Therefore, 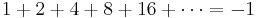 .
.
The error in such "proofs" is the implicit assumption that divergent series obey the ordinary laws of arithmetic.
Power and root
Fallacies involving disregarding the rules of elementary arithmetic through an incorrect manipulation of the radical. For complex numbers the failure of power and logarithm identities has led to many fallacies.
Positive and negative roots
Invalid proofs utilizing powers and roots are often of the following kind:[7]
The fallacy is that the rule 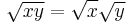 is generally valid only if at least one of the two numbers x or y is positive, which is not the case here.
is generally valid only if at least one of the two numbers x or y is positive, which is not the case here.
Although the fallacy is easily detected here, sometimes it is concealed more effectively in notation. For instance,[8] consider the equation
which holds as a consequence of the Pythagorean theorem. Then, by taking a square root,
so that
But evaluating this when x = π implies
or
which is absurd.
The error in each of these examples fundamentally lies in the fact that any equation of the form
has two solutions, provided a ≠ 0,
and it is essential to check which of these solutions is relevant to the problem at hand.[9] In the above fallacy, the square root that allowed the second equation to be deduced from the first is valid only when cos x is positive. In particular, when x is set to π, the second equation is rendered invalid.
Another example of this kind of fallacy, where the error is immediately detectable, is the following invalid proof that −2 = 2. Letting x = −2, and then squaring gives
whereupon taking a square root implies
so that x = −2 = 2, which is absurd. Clearly when the square root was extracted, it was the negative root −2, rather than the positive root, that was relevant for the particular solution in the problem.
Alternatively, imaginary roots are obfuscated in the following:
The error here lies in the last equality, where we are ignoring the other fourth roots of 1,[10] which are −1, i and −i (where i is the imaginary unit). Seeing as we have squared our figure and then taken roots, we cannot always assume that all the roots will be correct. So the correct fourth are i and −i, which are the imaginary numbers defined to be 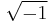 .
.
Complex exponents
When a number is raised to a complex power, the result is not uniquely defined (see Failure of power and logarithm identities). If this property is not recognized, then errors such as the following can result:
The error here is that the rule of multiplying exponents as when going to the third line does not apply unmodified with complex exponents, even if when putting both sides to the power i only the principle value is chosen. When treated as multivalued functions, both sides produce the same set of values, being {e2πn | n ∈ ℤ}.
Extraneous solutions
We are going to prove that 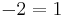 . Start by attempting to solve the equation
. Start by attempting to solve the equation
Taking the cube of both sides yields
Replacing the expression within parenthesis by the initial equation and canceling common terms yields
Taking the cube again produces
Which produces the solution x = 2. Substituting this value into the original equation, one obtains
So therefore
Q.E.D.
In the forward direction, the argument merely shows that no x exists satisfying the given equation. If you work backward from 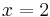 , taking the cube root of both sides ignores the possible factors of
, taking the cube root of both sides ignores the possible factors of 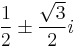 which are non-principal cube roots of negative one. An equation altered by raising both sides to a power is a consequence, but not necessarily equivalent to, the original equation, so it may produce more solutions. This is indeed the case in this example, where the solution x = 2 is arrived at while it is clear that this is not a solution to the original equation. Also, every number has 3 cube roots, 2 complex and one either real or complex. Also the substitution of the first equation into the second to get the third would be begging the question when working backwards.
which are non-principal cube roots of negative one. An equation altered by raising both sides to a power is a consequence, but not necessarily equivalent to, the original equation, so it may produce more solutions. This is indeed the case in this example, where the solution x = 2 is arrived at while it is clear that this is not a solution to the original equation. Also, every number has 3 cube roots, 2 complex and one either real or complex. Also the substitution of the first equation into the second to get the third would be begging the question when working backwards.
Complex roots
We are going to prove that 3 = 0. Assume the following equation for a complex x:
Then:
Divide by x (x ≠ 0 because x = 0 does not satisfy the original equation)
Substituting the last expression for x in the original equation we get:
Substituting 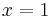 in the original equation yields:
in the original equation yields:
Q.E.D.
The fallacy here is in assuming that 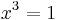 implies
implies 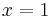 . There are in fact three cube roots of unity. Two of these roots, which are complex, are the solutions of the original equation. The substitution has introduced the third one, which is real, as an extraneous solution. The equation after the substitution step is implied by the equation before the substitution, but not the other way around, which means that the substitution step could and did introduce new solutions.
. There are in fact three cube roots of unity. Two of these roots, which are complex, are the solutions of the original equation. The substitution has introduced the third one, which is real, as an extraneous solution. The equation after the substitution step is implied by the equation before the substitution, but not the other way around, which means that the substitution step could and did introduce new solutions.
Note that if we restrict our attention to the real numbers, so that 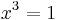 implies
implies 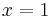 is in fact true, the proof will still fail. In fact, what it is saying is that if there is some real number solution to the equation, then 0 = 3. This implication is true, so the fact that 0 ≠ 3 implies that no real solution exists. This can be shown by the quadratic formula.
is in fact true, the proof will still fail. In fact, what it is saying is that if there is some real number solution to the equation, then 0 = 3. This implication is true, so the fact that 0 ≠ 3 implies that no real solution exists. This can be shown by the quadratic formula.
Fundamental theorem of algebra
The fundamental theorem of algebra applies for any polynomial defined for complex numbers. Ignoring this can lead to mathematical fallacies.
Let x and y be any two numbers; we are going to prove that they are the same.
Let 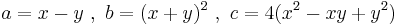
Let 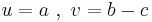
Let's compute:
Replacing 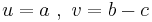 , we get:
, we get:
Let's compute 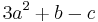 Replacing
Replacing 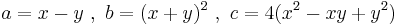 :
:
So:
Replacing 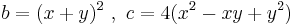 :
:
Q.E.D.
The mistake here is that from z3 = w3 one may not in general deduce z = w (unless z and w are both real, which they are not in our case).
Inequalities
Inequalities can lead to mathematical fallacies when operations that fail to preserve the inequality are not recognized.
We are going to prove that 1<0. Let us first suppose that there is an x such that:
Now we will take the logarithm of both sides. As long as x > 0, we can do this because logarithms are monotonically increasing. Observing that the logarithm of 1 is 0, we get
Dividing by ln (x) gives
Q.E.D.
The violation is found in the last step, the division. This step is invalid because ln(x) is negative for 0 < x < 1. While multiplication or division by a positive number preserves the inequality, multiplication or division by a negative number reverses the inequality, resulting in the correct expression 1 > 0.
Geometry
Many mathematical fallacies based on geometry come from assuming a geometrically impossible situation. Often the fallacy is easy to expose through simple visualizations.
Any angle is zero
Construct a rectangle ABCD. Now identify a point E such that CD = CE and the angle DCE is a non-zero angle. Take the perpendicular bisector of AD, crossing at F, and the perpendicular bisector of AE, crossing at G. Label where the two perpendicular bisectors intersect as H and join this point to A, B, C, D, and E.
Now, AH=DH because FH is a perpendicular bisector; similarly BH = CH. AH=EH because GH is a perpendicular bisector, so DH = EH. And by construction BA = CD = CE. So the triangles ABH, DCH and ECH are congruent, and so the angles ABH, DCH and ECH are equal.
But if the angles DCH and ECH are equal then the angle DCE must be zero, which is a contradiction.
The error in the proof comes in the diagram and the final point. An accurate diagram would show that the triangle ECH is a reflection of the triangle DCH in the line CH rather than being on the same side, and so while the angles DCH and ECH are equal in magnitude, there is no justification for subtracting one from the other; to find the angle DCE you need to subtract the angles DCH and ECH from the angle of a full circle (2π or 360°).
Fallacy of the isosceles triangle
The fallacy of the isosceles triangle, from (Maxwell 1959, Chapter II, § 1), purports to show that every triangle is isosceles, meaning that two sides of the triangle are congruent. This fallacy has been attributed to Lewis Carroll.[11]
Given a triangle △ABC, prove that AB = AC:
- Draw a line bisecting ∠A
- Call the midpoint of line segment BC, D
- Draw the perpendicular bisector of segment BC, which contains D
- If these two lines are parallel, AB = AC; otherwise they intersect at point O
- Draw line OR perpendicular to AB, line OQ perpendicular to AC
- Draw lines OB and OC
- By AAS, △RAO ≅ △QAO (AO = AO; ∠OAQ ≅ ∠OAR since AO bisects ∠A; ∠ARO ≅ ∠AQO are both right angles)
- By SAS, △ODB ≅ △ODC (∠ODB,∠ODC are right angles; OD = OD; BD = CD because OD bisects BC)
- By HL, △ROB ≅ △QOC (RO = QO since △RAO ≅ △QAO; BO = CO since △ODB ≅ △ODC; ∠ORB and ∠OQC are right angles)
- Thus, AR ≅ AQ, RB ≅ QC, and AB = AR + RB = AQ + QC = AC
Q.E.D.
As a corollary, one can show that all triangles are equilateral, by showing that AB = BC and AC = BC in the same way.
All but the last step of the proof is indeed correct (those three pairs of triangles are indeed congruent). The error in the proof is the assumption in the diagram that the point O is inside the triangle. In fact, whenever AB ≠ AC, O lies outside the triangle. Furthermore, it can be further shown that, if AB is longer than AC, then R will lie within AB, while Q will lie outside of AC (and vice versa). (Any diagram drawn with sufficiently accurate instruments will verify the above two facts.) Because of this, AB is still AR + RB, but AC is actually AQ − QC; and thus the lengths are not necessarily the same.
See also
Notes
- ^ Fallacies in mathematics. Cambridge, UK: Cambridge University Press. 1963. ISBN 0-521-02640-7.
- ^ Maxwell 1959, p. 9
- ^ Maxwell 1959
- ^ Heath & Helberg 1908, Chapter II, §I
- ^ Maxwell 1959
- ^ Harro Heuser: Lehrbuch der Analysis - Teil 1, 6th edition, Teubner 1989, ISBN 978-3835101319, page 51 (German).
- ^ Maxwell 1959, Chapter VI, §I.2
- ^ Maxwell 1959, Chapter VI, §I.1
- ^ Maxwell 1959, Chapter VI, §II
- ^ In general, the expression
![\sqrt[n]{1}](/2012-wikipedia_en_all_nopic_01_2012/I/a5a1bedf31964af3498c3ed01de7177c.png) evaluates to n complex numbers, called the nth roots of unity.
evaluates to n complex numbers, called the nth roots of unity. - ^ Robin Wilson (2008). Lewis Carroll in Numberland. Penguin Books. pp. 169–170. ISBN 978-0-141-01610-8.
References
- Barbeau, Edward J. (2000), Mathematical fallacies, flaws, and flimflam, MAA Spectrum, Mathematical Association of America, ISBN 978-0-88385-529-4, MR1725831.
- Bunch, Bryan (1997), Mathematical fallacies and paradoxes, New York: Dover Publications, ISBN 978-0-486-29664-7, MR1461270.
- Heath, Sir Thomas Little; Heiberg, Johan Ludvig (1908), The thirteen books of Euclid's Elements, Volume 1, The University Press.
- Maxwell, E. A. (1959), Fallacies in mathematics, Cambridge University Press, MR0099907.
External links
- Invalid proofs at Cut-the-knot (including literature references)
- More invalid proofs from AhaJokes.com
- More invalid proofs also on this page
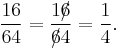
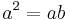
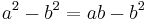
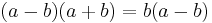
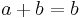
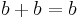
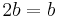
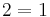
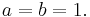
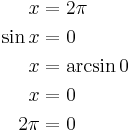
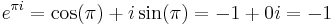
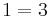
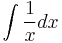
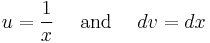
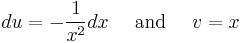
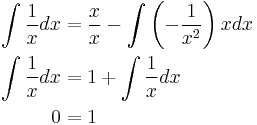
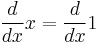
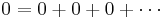
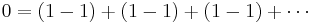
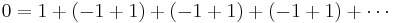
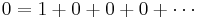
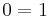

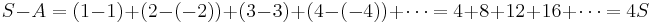
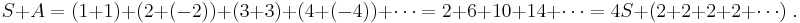
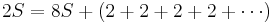
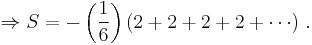
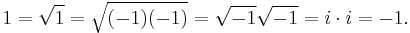
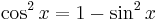
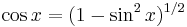
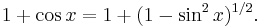
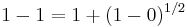
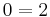
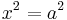
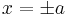
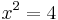
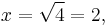
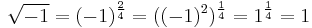
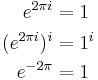
![\sqrt[3] {1-x} %2B \sqrt[3] {x-3} = 1\,](/2012-wikipedia_en_all_nopic_01_2012/I/10e278614064d15d3048b3c45b6d5c83.png)
![(1-x) %2B 3 \sqrt[3]{1-x} \ \sqrt[3]{x-3} \ (\sqrt[3]{1-x} %2B \sqrt[3]{x-3}) %2B (x-3) = 1\,](/2012-wikipedia_en_all_nopic_01_2012/I/dd0ba2c0c1618ddba2dab51629df18c5.png)
![\begin{align}
-2 %2B 3 \sqrt[3]{1-x} \ \sqrt[3]{x-3} &= 1 \\
\sqrt[3]{1-x} \ \sqrt[3]{x-3} &= 1 \\
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/539a6ad160161332b2cb1cd67fe49cc2.png)
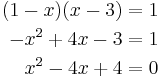
![\sqrt[3] {1-2} %2B \sqrt[3] {2-3} = 1\,](/2012-wikipedia_en_all_nopic_01_2012/I/f002b74f3a0e24bb4e1c5a8fc52e2f9d.png)